For the numerical implementation, the shape model of asteroid Didymos (Figure 1) have been used to compute its induced gravity field. The corresponding shape model consists of 1,000 vertices and 1,996 triangular faces. The total volume of Didymos equals to 0.24855 km^3 and its density is set to 2140.668 km/m^3. To evaluate the gravity signal of Didymos, the line integral analytical approach of general polyhedron has been applied. The calculations are performd on a set of 24,389 3D points that create a total of 29 grid planes parallel to the X = 0 Cartesian plane (Figure 2). The results are illustrated in the 2D maps shown in Figure 3. The same gravitational values can be computed numerically, using their expressions into spherical harmonic series. The normalized spherical harmonic coefficients that participate in those series, up to maximum expansion degree 100 for asteroid Didymos are shown in the triangular plot of Figure 4.
Figure 1. Asteroid Didymos from three different perspectives.
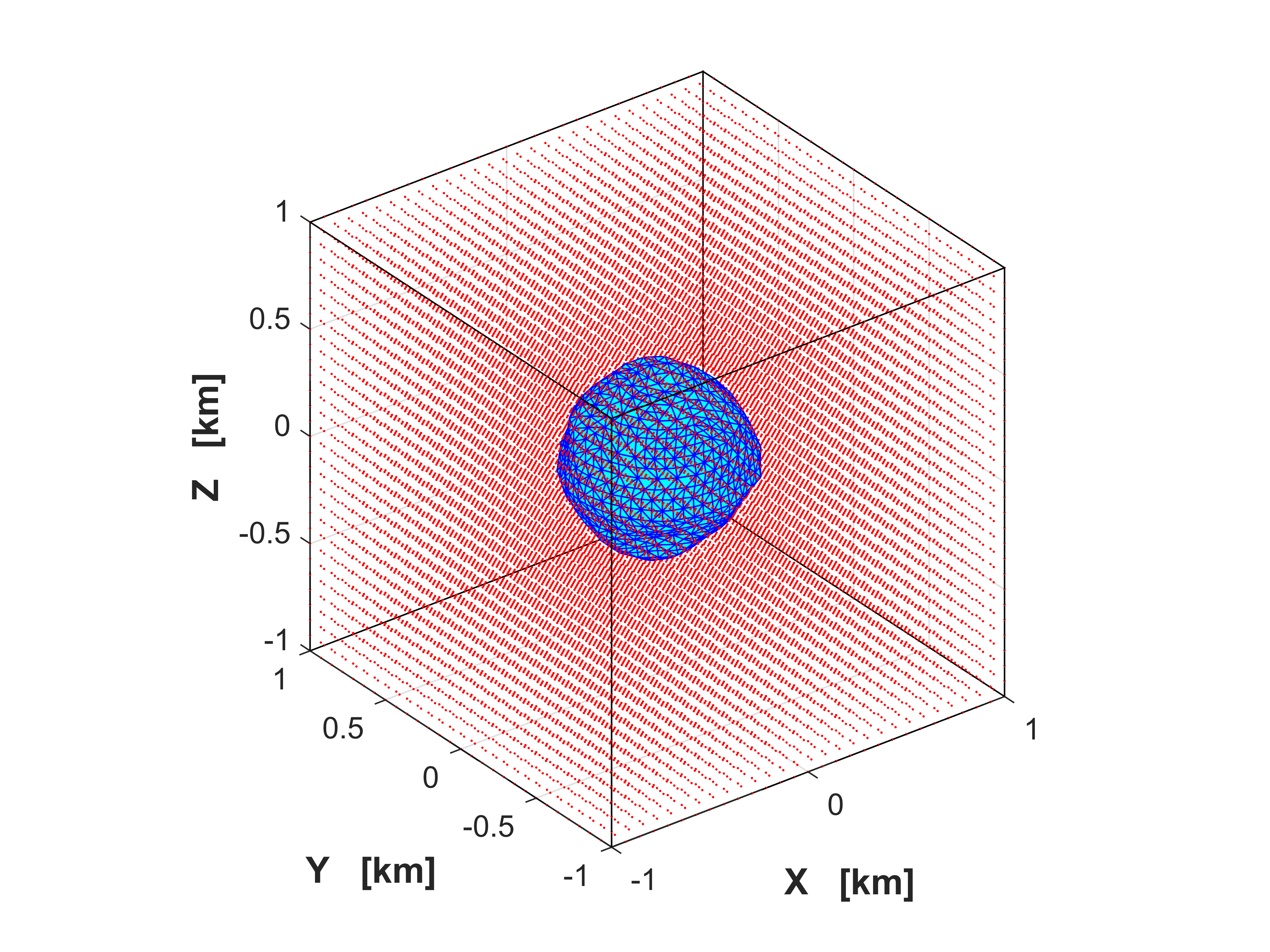
Figure 2. Asteroid Disdymos and the applied 3D computation points illustrated with red color, located inside a theoretical box of dimensions 2 km x 2 km x 2 km.
Figure 3. Gravitational potential (1st column) with its first order derivatives Vx (2nd column), Vy (3rd column), Vz (4th column) induced by asteroid Didymos on 5 planes parallel to the X = 0 Cartesian plane. The 1st row refer to ΔΧ = -0.857143 km plane, 2nd to ΔΧ = -0.642857 km, 3rd to ΔΧ = -0.428571 km, 4th to ΔΧ = -0.214286 km and 5th to ΔΧ = 0 km. The units are given in m^(2)s^(-2) for gravitational potential and ms^(-2) for its first order derivatives. The computation of the corresponding gravitational values is based on the line integral analytical method of general polyhedron.
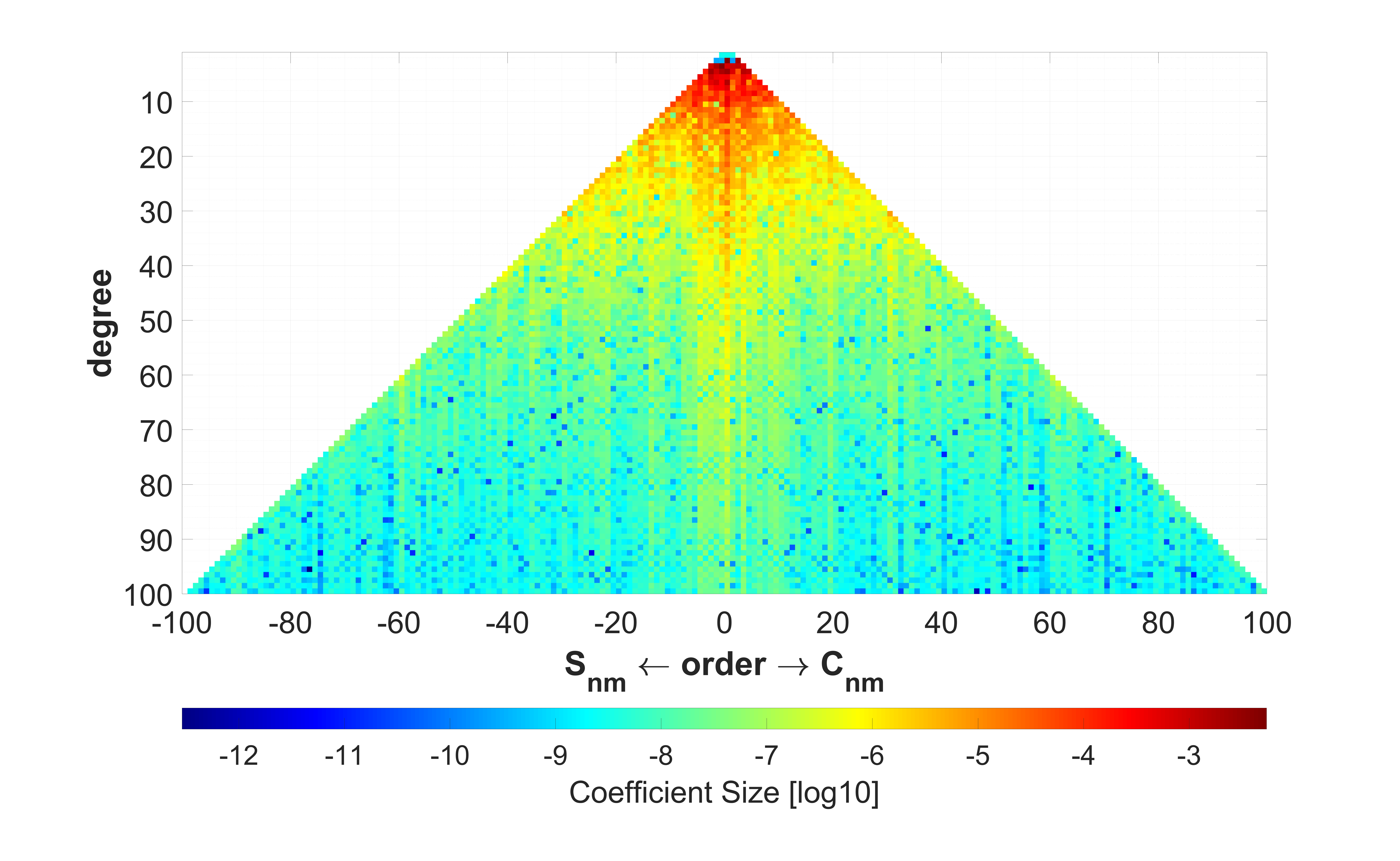
Figure 4. Triangular plot of normalized spherical harmonic coefficients for asteroid Didymos up to maximum expansion degree 100.

